서로소 집합 자료구조, 합집합-찾기 자료구조 개념이 필요하기 때문에 잘 모른다면 아래에서 읽어보고 오는 것이 좋다.
2022.03.05 - [정보[Information]] - 서로소 집합 자료구조(Union-Find)(Python-파이썬)
서로소 집합 자료구조(Union-Find)(Python-파이썬)
서로소 집합(Disjoint Sets) 수학에서 서로소 집합(Disjoint Sets)이란 공통 원소가 없는 두 집합을 의미한다. 예를 들어 집합 {1,2} 와 집합 {3,4}는 서로소 관계이다. 반면에 집합 {1,2}와 집합 {2,3}은 2라는.
soopeach.tistory.com
신장 트리
신장 트리는 그래프 알고리즘 문제로 자주 출제되는 문제 유형이다.
기본적으로 신장 트리(Spanning Tree)란 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다. 이때 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 성립 조건이기도 하다. 그래서 이런 그래프를 신장 트리라고 부른다.
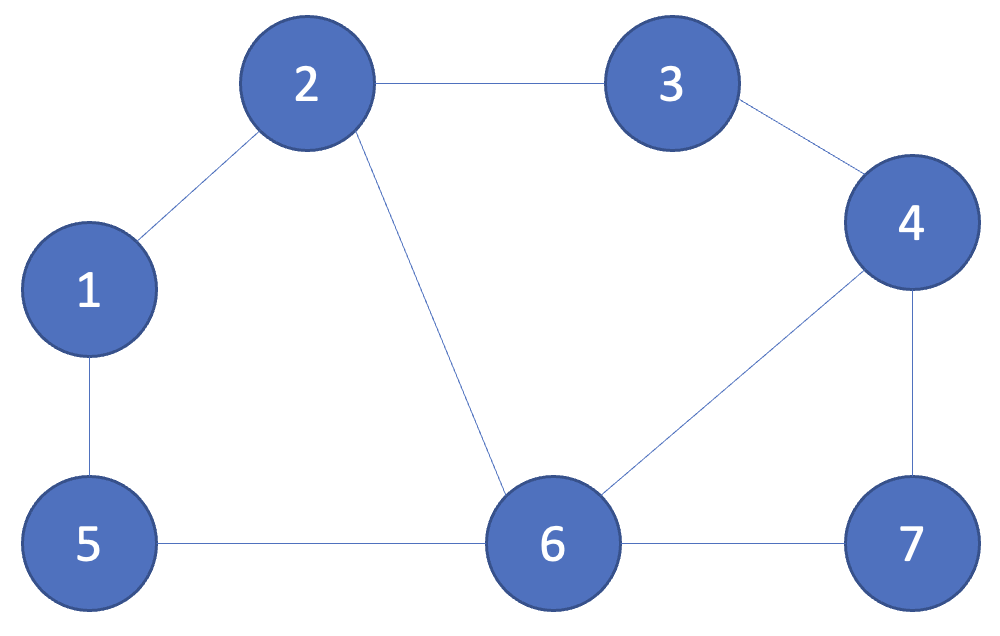
위와 같은 그래프가 있다고 하자. 위의 그래프에서는 여러 개의 신장 트리를 찾을 수 있다.
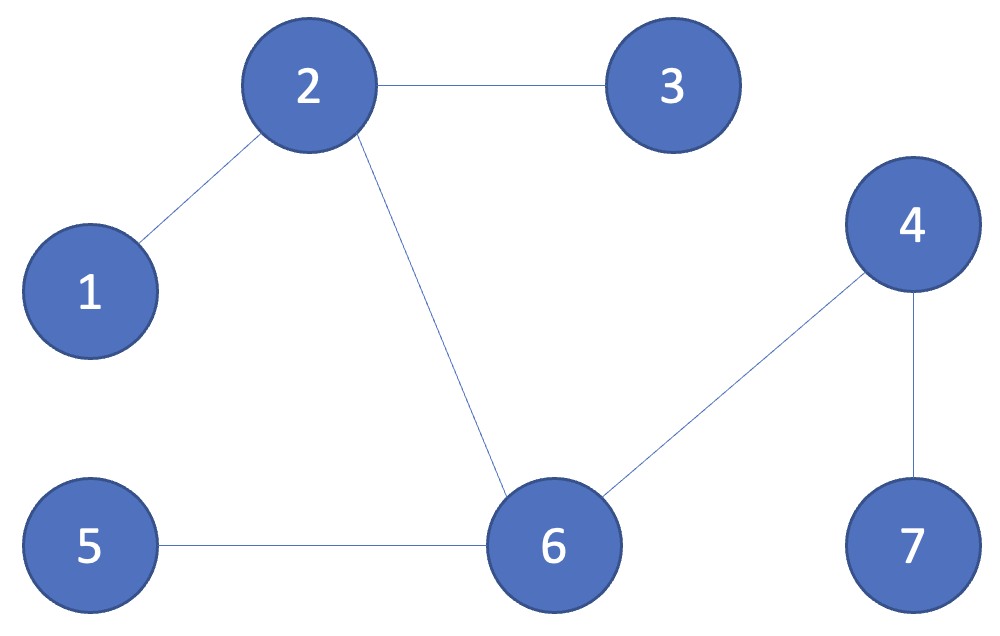
이 그래프가 위의 그래프에서 찾을 수 있는 여러가지의 신장 트리 중 하나이다.

이 그래프는 둘다 신장 트리에 해당하지 않는다.
왼쪽 그림은 그래프가 '노드 1'을 포함하고 있지 않기 때문이고 오른쪽 그림은 '노드 4, 6, 7'간 사이클이 존재하기 때문에 신장 트리가 아니다.
크루스칼 알고리즘(Kruskal Algorithm)
우리는 다양한 문제 상황에서 가능한 한 최소한의 비용으로 신장 트리를 찾아야 할 때가 있다.
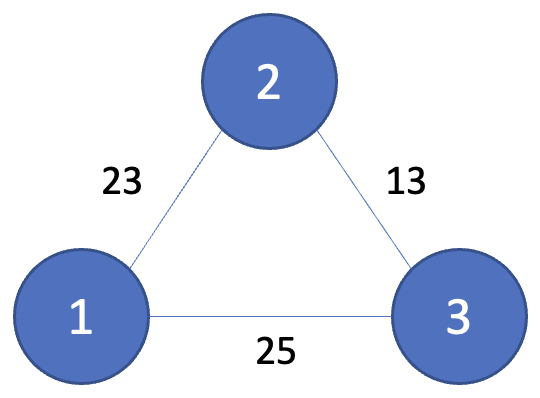
위와 같은 그래프가 있다고 해보자.
1, 2, 3 총 3개의 도시가 있다.
1번과 2번 도시 간에는 23의 비용이 들고 2번과 3번 도시 간에는 13의 비용이 들고 1번과 3번 도시 간에는 25의 비용이 든다.
여기서 1, 2,3 도시를 모두 이동할 수 있도록 연결하기 위해 가장 최소한의 비용을 가지는 신장 트리는 36이다.
총 3가지의 경우로 신장 트리를 구할 수 있는데 아래와 같다.
1번 경우 1-2 + 2-3 = 23 + 13 = 36
2번 경우 1-2 + 1-3 = 23 + 25 = 48
3번 경우 1-3 + 2-3 = 25 + 13 = 38
따라서 1번 경우가 최소 신장 트리임을 알 수 있다.
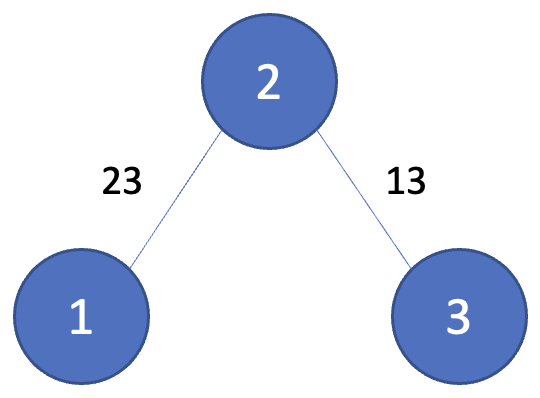
이 그래프는 위의 그래프에서 찾을 수 있는 1번 경우로 만들어진 최소 신장 트리 그래프이다.
이처럼 신장 트리 중에서 최소 비용으로 만들 수 있는 신장 트리를 찾는 알고리즘을 '최소 신장 트리 알고리즘' 이라고 한다.
대표적인 최소 신장 트리 알고리즘으로는 크루스칼 알고리즘(Kruskal Algorithm)이 있다.
크루스칼 알고리즘을 사용하면 가장 적은 비용으로 모든 노드를 연결할 수 있는데 크루스칼 알고리즘은 그리디 알고리즘으로 분류된다.
먼저 모든 간선에 대하여 정렬을 수행한 뒤에 가장 거리가 짧은 간선부터 집합에 포함시키면 된다. 이때 사이클을 발생시킬 수 있는 간선의 경우, 집합에 포함시키지 않는다.
아래는 크루스칼 알고리즘의 과정이다.
1. 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
2-1. 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
2-2. 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
3. 모든 간선에 대하여 2번의 과정을 반복한다.
다음 그래프의 최소 신장 트리를 구해보자.

위의 그래프에서 찾을 수 있는 최소 신장 트리는 다음과 같다.
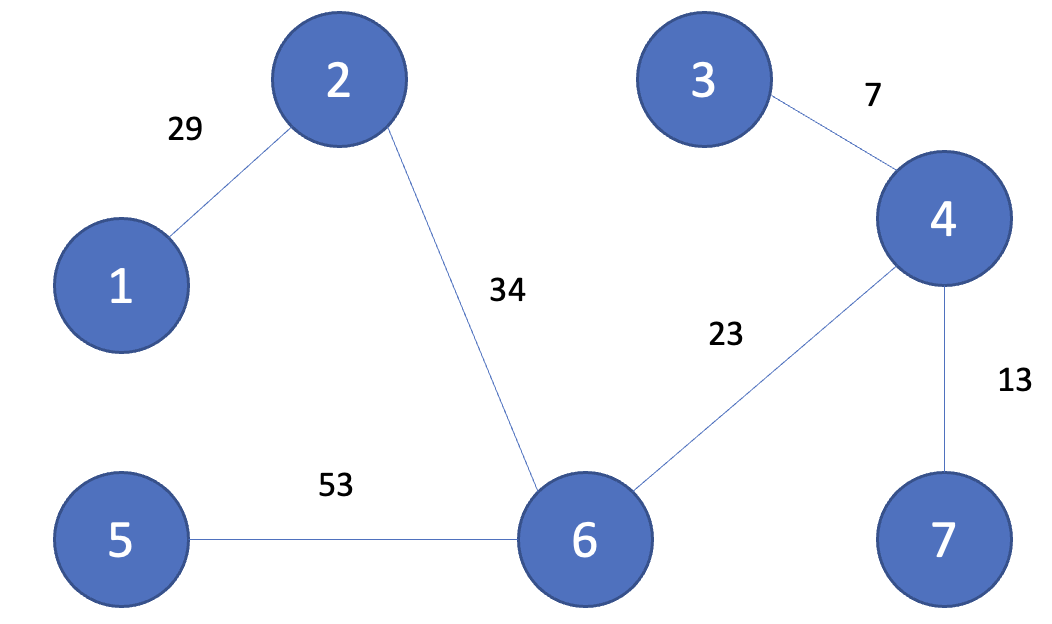
최소 신장 트리는 일종의 트리(Tree) 자료구조이므로, 최종적으로 신장 트리에 포함되는 간선의 개수가 '노드의 개수 - 1'과 같다는 특징이 있다. 예를 들어 위의 예시에서는 노드의 개수가 7이고 간선의 개수가 6이다.
따라서 크루스칼 알고리즘의 핵심 원리는 가장 거리가 짧은 간선부터 차례대로 집합에 추가하면 된다는 것이다.
단, 사이클을 발생시키는 간선은 제외하고 연결해야한다. 이렇게 하면 항상 최적의 해를 보장할 수 있다.
크루스칼 알고리즘을 이용하여 최소 신장 트리를 찾는 과정을 단계별로 확인해보자.
크루스칼 알고리즘(Kruskal Algorithm) 과정
아래의 그래프로 크루스칼 알고리즘 과정을 진행해보겠다.

초기 단계에서는 그래프의 모든 간선 정보만 따로 빼내어 정렬을 수행한다. 알고리즘 코드를 작성할 때에는 비용에 따라 오름차순으로 정렬하지만 설명하는 과정에서는 노드 데이터 순서에 따라 데이터를 정리하였다.

위와 같이 가독성을 위해 노드 데이터 순으로 테이블을 정리하였다.
가장 짧은 간선부터 계속 확인한다.
Step 1
첫번째 단계에서는 가장 짧은 간선인 (3, 4)가 선택되고 노드 3과 노드 4는 같은 집합에 속하지 않기 때문에 집합에 포함시킨다. union(3, 4)을 한다는 의미이다. 처리가 된 간선은 빨간 선으로 표시하겠다.
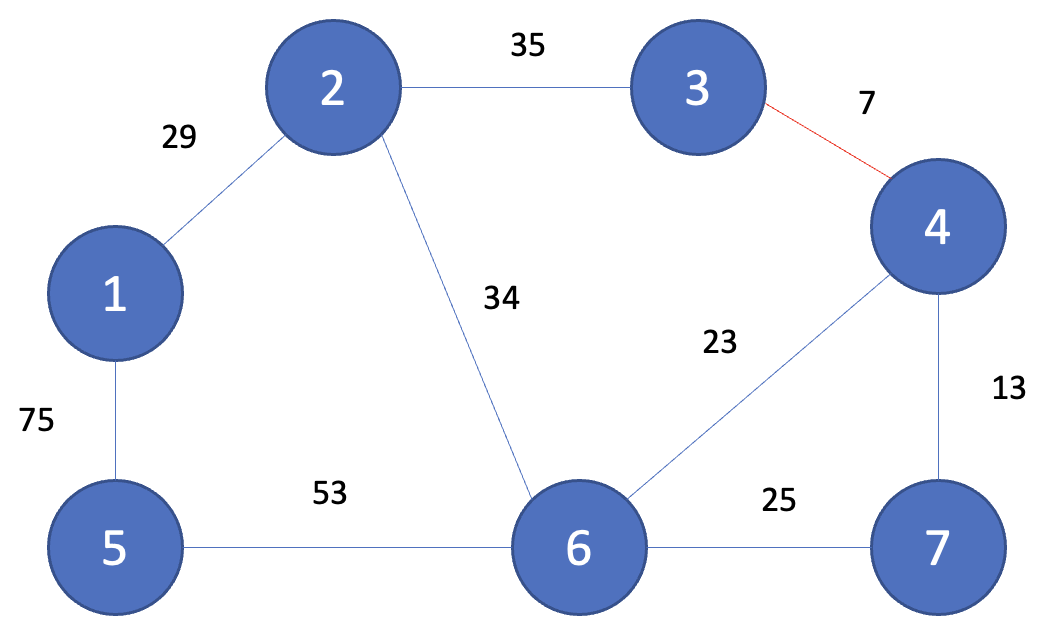

Step 2
그다음으로 짧은 간선인 (4, 7)이 선택되고 노드 4와 노드 7은 같은 집합에 속하지 않기 때문에 union(4, 7)을 해준다.
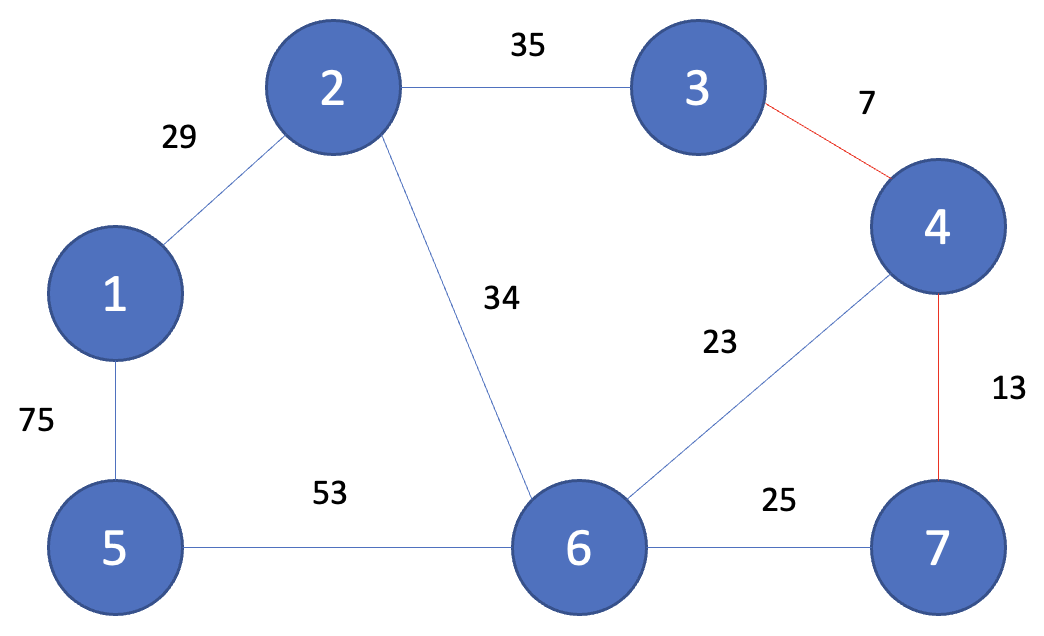

Step 3
그다음으로 짧은 간선인 (4, 6)이 선택되고 노드 4와 노드 6은 같은 집합에 속하지 않기 때문에 union(4, 6)을 해준다.


Step 4
그다음으로 짧은 간선인 (6, 7)이 선택된다. 노드 6과 노드 7의 루트 노드를 확인해보면 이미 동일한 집합에 포함되어 있기 때문에 신장 트리에 포함하지 않아야 한다. 따라서 union(6, 7)을 하지 않는다.
처리가 되었지만 신장 트리에 포함되지 않는 간선은 점선으로 표시하겠다.


Step 5
그다음으로 짧은 간선인 (1, 2)가 선택되고 노드 1과 노드 2는 같은 집합에 속하지 않기 때문에 union(1, 2)을 해준다.
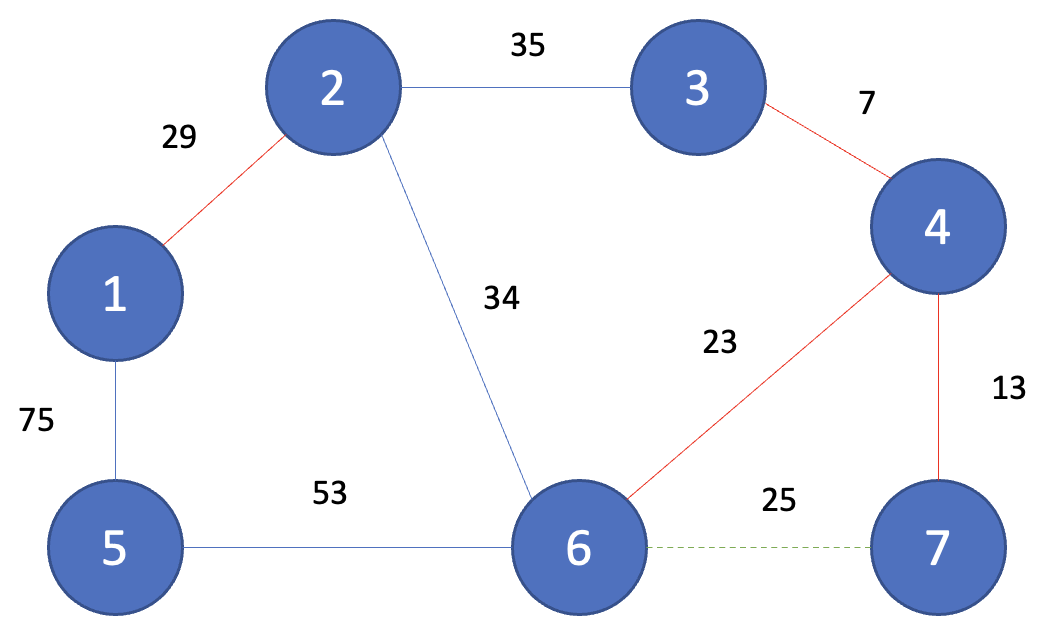

Step 6
그다음으로 짧은 간선인 (2, 6)이 선택되고 노드 2와 노드 6은 같은 집합에 속하지 않기 때문에 union(2, 6)을 해준다.
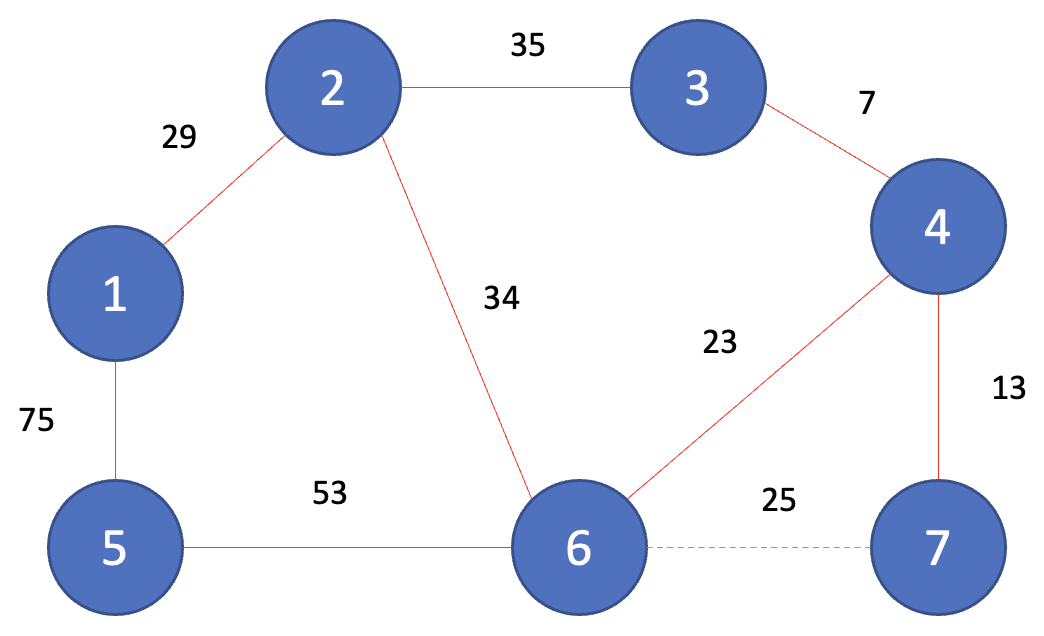

Step 7
그다음으로 짧은 간선인 (2, 3)이 선택되고 노드 2와 노드 3은 같은 집합에 속하기 때문에 union(2, 3)을 하지 않는다.
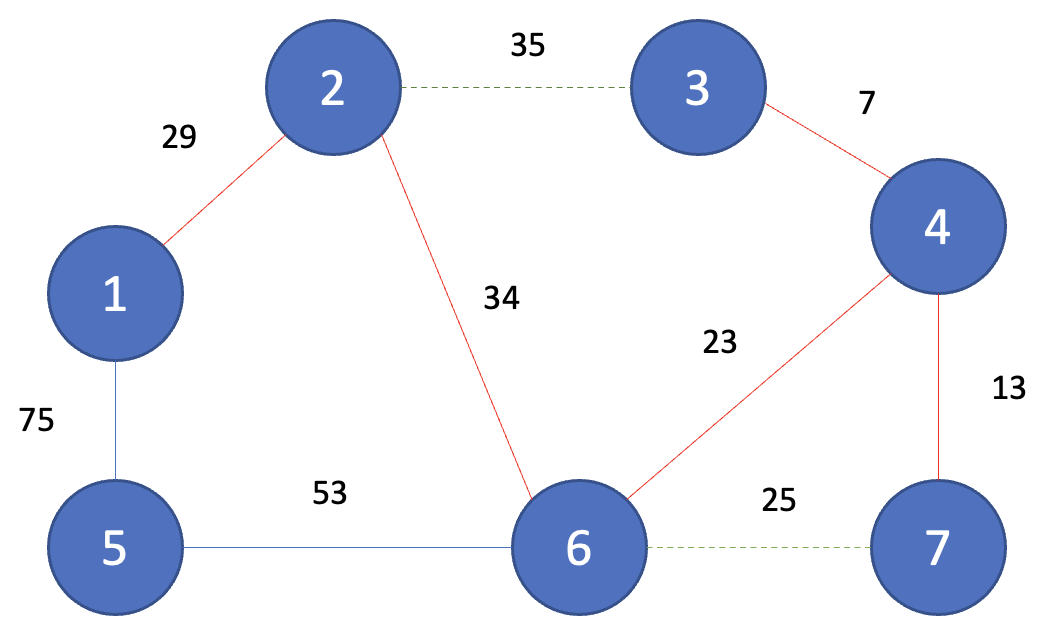

Step 8
그다음으로 짧은 간선인 (5, 6)이 선택되고 노드 5와 노드 6은 같은 집합에 속하지 않기 때문에 union(5, 6)을 해준다.


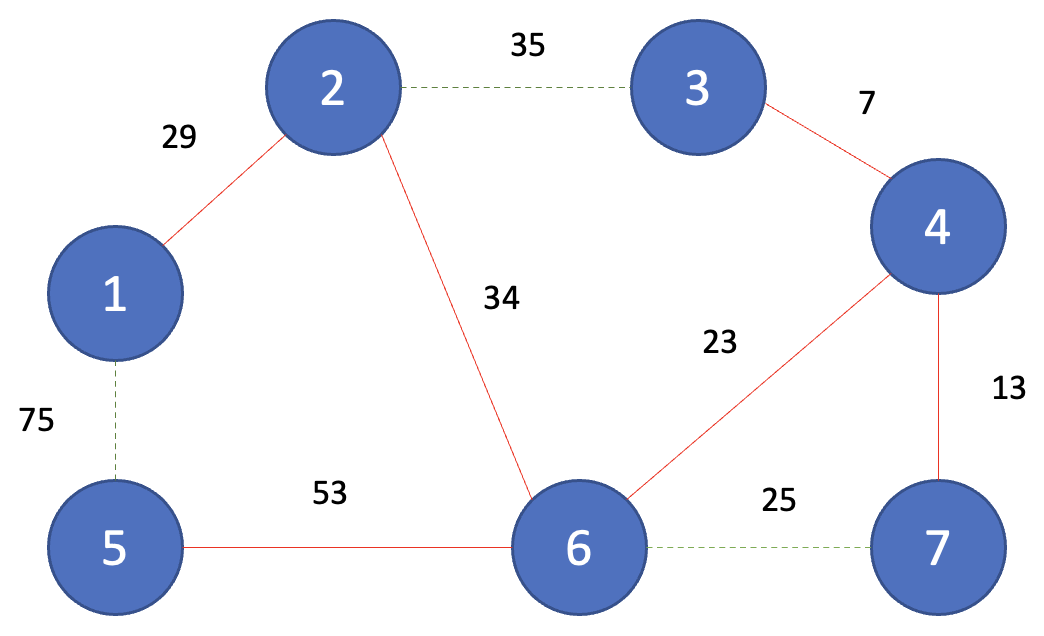
Step 9
그다음으로 짧은 간선이자 마지막 간선인 (1, 5)과 선택되고 노드 1과 노드 5는 같은 집합에 속하기 때문에 union(1, 5)을 하지 않는다.

결과적으로 아래와 같은 최소 신장 트리가 나오게 된다.
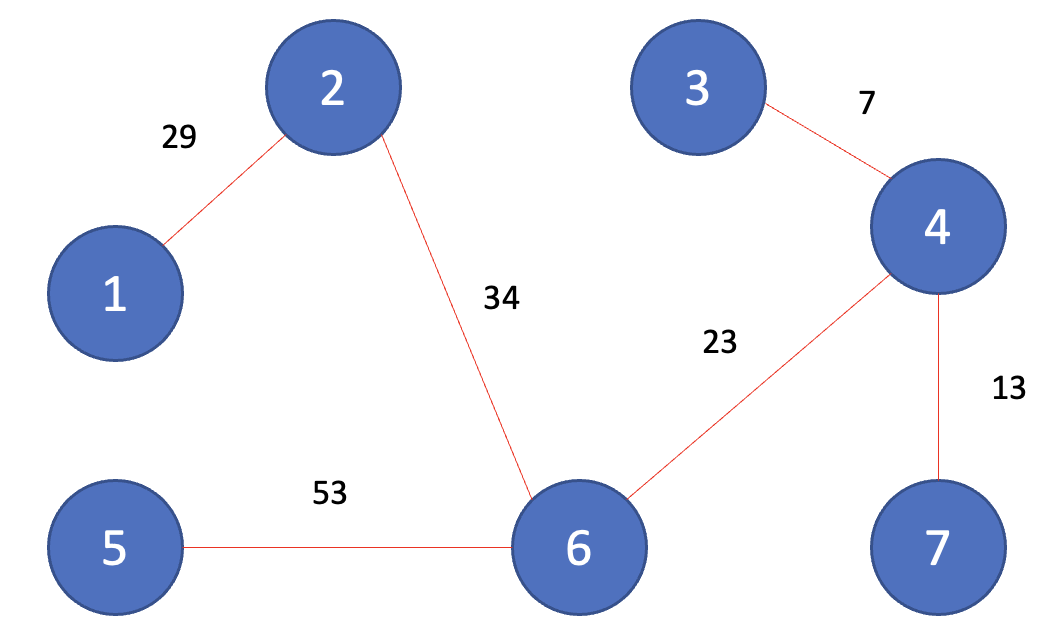
최소 신장 트리에 포함되어 있는 간선의 비용만 모두 더하면, 그 값이 최종 비용에 해당된다. 위의 예시에서는 총비용이 159가 된다.
이렇게 최소 신장 트리를 만드는데 필요한 비용을 계산하는 크루스칼 알고리즘의 소스코드는 다음과 같다.
크루스칼 알고리즘(Kruskal Algorithm) 소스 코드
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x) :
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b :
parent[b] = a
else :
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int,input().split())
parent = [0] * (v+1)
# 모든 간선을 담을 리스트와 최종 비용을 담을 변수
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1) :
parent[i] = i
# 모든 간선에 대한 정보를 입력받기
for _ in range(e) :
a, b, cost = map(int,input().split())
# 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b) :
union_parent(parent,a , b)
result += cost
print(result)# input
7 9
1 2 29
1 5 75
2 3 35
2 6 34
3 4 7
4 6 23
4 7 13
5 6 53
6 7 25
# output
159크루스칼 알고리즘(Kruskal Algorithm)의 시간 복잡도
크루스칼 알고리즘은 간선의 개수가 E개일 때, O(ElogE)의 시간 복잡도를 가진다.
크루스칼 알고리즘에서 시간이 가장 오래 걸리는 부분이 간선을 정렬하는 작업이며, E개의 데이터를 정렬했을 때의 시간 복잡도는 O(ElogE)이기 때문이다.
크루스칼 내부에서 사용되는 서로소 집합 알고리즘의 시간 복잡도는 정렬 알고리즘의 시간 복잡도보다 작으므로 무시한다.
'정보[Information]' 카테고리의 다른 글
| 자바[Java] 오버로딩과 오버라이딩(overloading Vs overriding) (0) | 2022.04.12 |
|---|---|
| HTML 블록 태그 / 인라인 태그 (Block Tag / Inline Tag) (0) | 2022.04.06 |
| 서로소 집합 자료구조(Union-Find)(Python-파이썬) (0) | 2022.03.05 |
| API(Application Programming Interface)란? (0) | 2022.02.20 |
| 클린 코드(Clean Code)를 작성하는 5가지 팁 (3) | 2022.01.23 |






최근댓글