서로소 집합(Disjoint Sets)
수학에서 서로소 집합(Disjoint Sets)이란 공통 원소가 없는 두 집합을 의미한다.
예를 들어 집합 {1,2} 와 집합 {3,4}는 서로소 관계이다. 반면에 집합 {1,2}와 집합 {2,3}은 2라는 공통 원소가 있으므로 서로소 집합이 아니다.
서로소 집합(Disjoint Sets) 자료구조 / 합집합-찾기(Union-Find) 자료구조
서로소 집합 자료구조는 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조라고 할 수 있다.
서로소 집합 자료구조는 union과 find 이 2개의 연산으로 조작할 수 있다.
union(합집합) 연산은 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산이다.
find(찾기) 연산은 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산이다.
스택과 큐가 각각 push, pop 연산으로 이루어졌던 것처럼, 서로소 집합 자료구조는 union, find 연산으로 구성된다.
서로소 집합(Disjoint Sets) 자료구조는 합집합-찾기(Union-Find) 자료구조라고 불리기도 한다.
서로소 집합 자료구조를 구현할 때에는 트리 자료구조를 이용하여 집합을 표현한다.
서로소 집합정보(합집합 연산)가 주어졌을 때 트리 자료구조를 이용해서 집합을 표현하는 서로소 집합 계산 알고리즘은 다음과 같다.
1. union(합집합) 연산을 확인하여, 서로 연결된 두 노드 A, B를 확인
1-1. A와 B의 루트 노드인 A', B'를 각각 찾는다.
1-2. A'를 B'의 부모 노드로 설정(B'의 번호가 더 작다면 B'를 A'의 부모 노드로 설정)
2. 모든 union(합집합) 연산을 처리할 때까지 1.번 과정을 반복
6개의 원소로 이루어진 {1, 2, 3, 4, 5, 6} 집합이 있고 union(1, 4), union(2, 3), union(2, 4), union(5, 6)이 있다고 가정을 해보자.
union(1, 4)는 '1과 4는 같은 집합'이라는 의미를 가진다.
이와 같은 union연산들은 그래프 형태로 표현이 가능하다.
{1, 2, 3, 4, 5, 6} 집합에 있는 원소들은 각각 1 ~ 6까지의 노드를 표현하고 union(1, 4)는 1과 4 사이의 간선이라고 표현할 수 있다.
즉 6개의 노드가 있고 4개의 간선이 있는 그래프라고 생각할 수 있다.
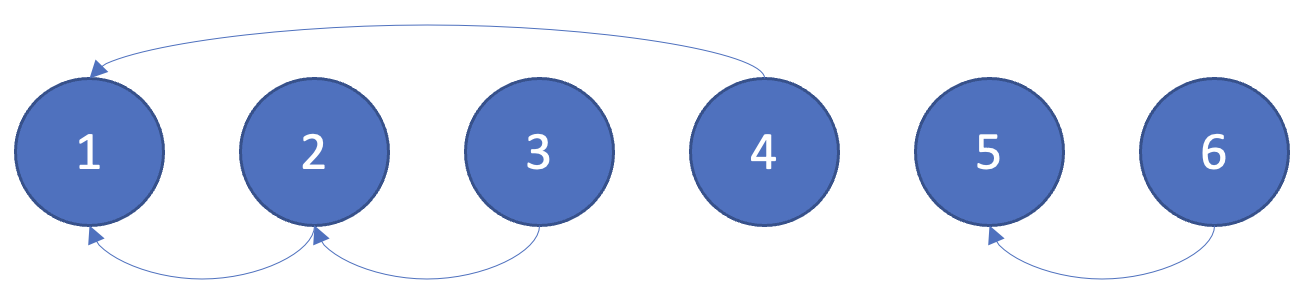
위의 4개의 합집합(union) 연산을 시행하고 나면 위와 같은 형태가 된다.
전체 원소가 {1, 2, 3, 4}와 {5, 6}인 두 집합으로 나누어진다는 것을 알 수 있다.
위의 그래프에서 3은 1과 간접적(2를 통하여) 연결이 되어있기 때문에 1과 같은 집합에 있다고 이해할 수 있다.
5는 1과의 연결성이 없기 때문에 서로 다른 집합으로 나누어져 있다고 이해할 수 있다.
Union-Find 과정
6개의 원소로 이루어진 {1, 2, 3, 4, 5, 6} 집합이 있고 union(1, 4), union(2, 3), union(2, 4), union(5, 6)이 있다.

union 연산을 하나씩 확인하면서 서로 다른 두 원소에 대해 합집합을 수행해야 할 때는, 각 루트 노드를 찾아서 더 큰 루트 노드가 작은 루트 노드를 가리키도록 한다.
가장 먼저 노드의 개수(V = 6) 만큼 부모 테이블을 초기화해준다. 그리고 모든 원소가 자기 자신을 부모로 가지도록 해준다.

첫번째 합집합 연산인 union(1, 4)를 확인해보면 1과 4를 합치게 된다. 노드 1과 노드 4의 루트 노드를 비교하였을 때 각각 1과 4이다.
더 큰 번호에 해당하는 루트 노드 4의 부모를 작은 번호인 1로 설정하여준다.
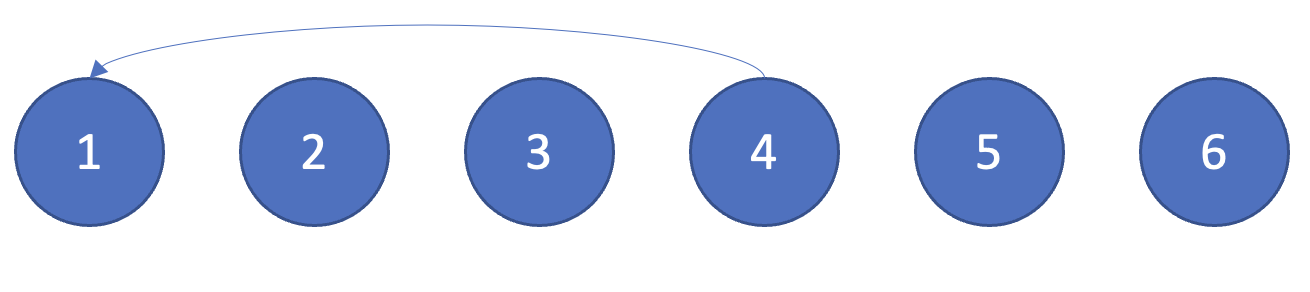

두번째 합집합 연산인 union(2, 3)을 확인하여 2와 3을 합치게 된다. 노드 2와 노드 3의 루트 노드는 각각 2와 3이므로 더 큰 번호에 해당하는 루트 노드 3의 부모를 2로 설정하여준다.
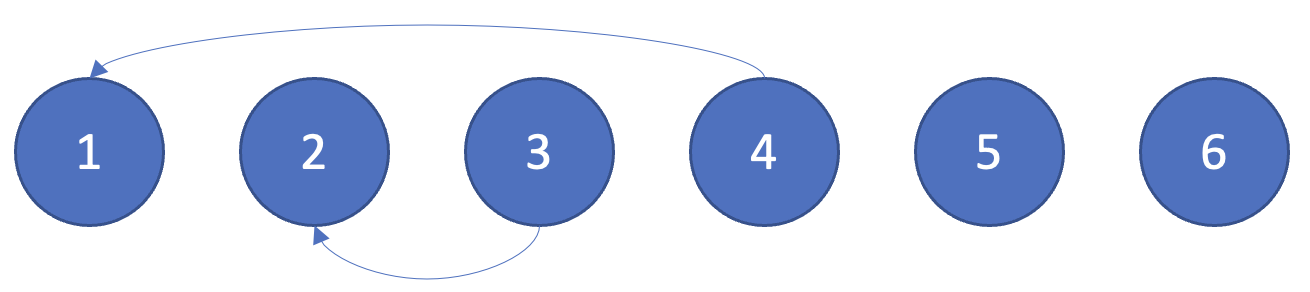

세번째 합집합 연산인 union(2, 4)을 확인하여 2와 4를 합치게 된다. 노드 2와 노드 4의 루트 노드는 각각 2와 1이기 때문에 더 큰 번호에 해당하는 루트 노드 2의 부모를 1로 설정하여준다.
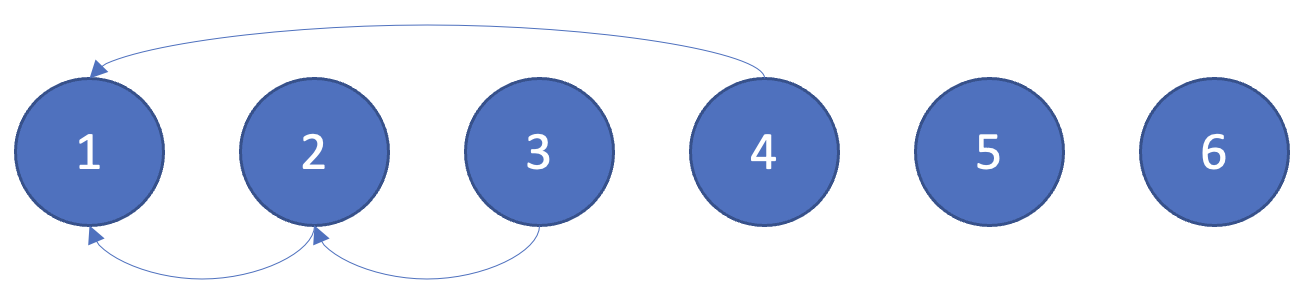

마지막 합집합 연산인 union(5, 6)을 확인하여 5와 6을 합치게 된다. 노드 5와 노드 6의 루트 노드는 각각 5와 6이기 때문에 더 큰 번호에 해당하는 루트 노드 6의 부모를 5로 설정하여준다.


모든 합집합 연산을 완료한 모습이다. 이 과정에서 유의할 점은 합집합 연산을 효과적으로 수행하기 위해 "부모 테이블"을 항상 가지고 있어야한다. 또한 루트 노드를 즉시 계산할 수 없고 부모 테이블을 확인하여 거슬러 올라가야한다.
예를 들면 3번 노드의 부모 노드는 2지만 2의 부모 노드는 1이기 때문의 3번 노드의 루트 노드는 1이라는 점에서 확인 할 수 있다.
따라서 서로소 집합 알고리즘으로 루트 노드를 찾기 위해서는 재귀적으로 부모를 거슬러 올라가는 과정이 필요하다.
위의 과정을 소스코드로 나타내면 아래와 같다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
return find_parent(parent, parent[x])
return x
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else :
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v+1)
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end="")
for i in range(1,v+1):
print(find_parent(parent,i), end=" ")
print()
# 부모 테이블 내용 출력
print("부모 테이블: ", end="")
for i in range(1, v+1):
print(parent[i], end=" ")find_parent 함수는 루트 노드를 찾는 함수이고 union_parent 함수는 union연산을 해주는 함수이다.
# input
6 4
1 4
2 3
2 4
5 6
# output
각 원소가 속한 집합: 1 1 1 1 5 5
부모 테이블: 1 1 2 1 5 5위의 소스코드에 input을 넣으면 output 결과가 출력된다.
이를 보고 전체 원소가 {1, 2, 3, 4}와 {5, 6}인 두 집합으로 나누어진다는 것을 알 수 있다.
다만 이렇게 구현하면 find함수가 비효율적으로 동작한다. 최악의 경우 find함수가 모든 노드를 다 확인하게 되어 시간 복잡도가 O(V)이 되게 된다.
{1, 2, 3, 4, 5}의 총 5개의 원소로 이루어진 집합이 있다고 가정해보자.
union연산이 순선대로 (4, 5),(3, 4),(2, 3),(1, 2)와 같이 주어졌을 때 차레대로 연산을 처리하게 된다면 아래와 같은 형태가 된다.


위의 그래프를 보면 알 수 있듯이 1~5까지의 모든 원소의 루트 노드는 1이다.
하지만 부모 테이블에 담겨있는 값은 순서대로 1, 1, 2, 3, 4이 된다.
노드 5의 루트 노드를 찾기 위해서는 노드 5 -> 노드 4 -> 노드 3 -> 노드 2 -> 노드 1 과정을 거쳐야 하기 때문의 최대 O(V)의 시간이 소요 된다.
현재의 알고리즘을 그대로 이용하게 된다면 노드의 개수가 V개이고 find 혹은 union 연산의 개수가 M개일 때, 전체 시간 복잡도는 O(VM)이 되어 비효율적이게 된다.
서로소 집합 알고리즘을 최적화하는 방법은 여러가지가 있지만 경로 압축(Path Compression)기법을 적용하여 find 함수를 아주 간단하게 최적화 할 수 있다.
경로 압축은 find 함수를 재귀적으로 호출한 뒤 부모 테이블 값을 갱신하는 기법이다.
기존의 비효율적인 find 함수
def find_parent(parent, x):
if parent[x] != x:
return find_parent(parent, parent[x])
return x경로 압축기법을 적용한 find 함수
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]이렇게 find 함수를 수정하게 된다면 find 함수를 호출한 이후 해당 노드의 루트 노드가 바로 부모 노드가 된다.
위의 예시와 동일하게
{1, 2, 3, 4, 5}의 총 5개의 원소로 이루어진 집합이 있고 union연산이 순선대로 (4, 5),(3, 4),(2, 3),(1, 2)와 같이 주어졌을 때
모든 union 함수를 처리한 후 각 원소에 대하여 find 함수를 수행하면 다음과 같이 부모 테이블이 형성된다.
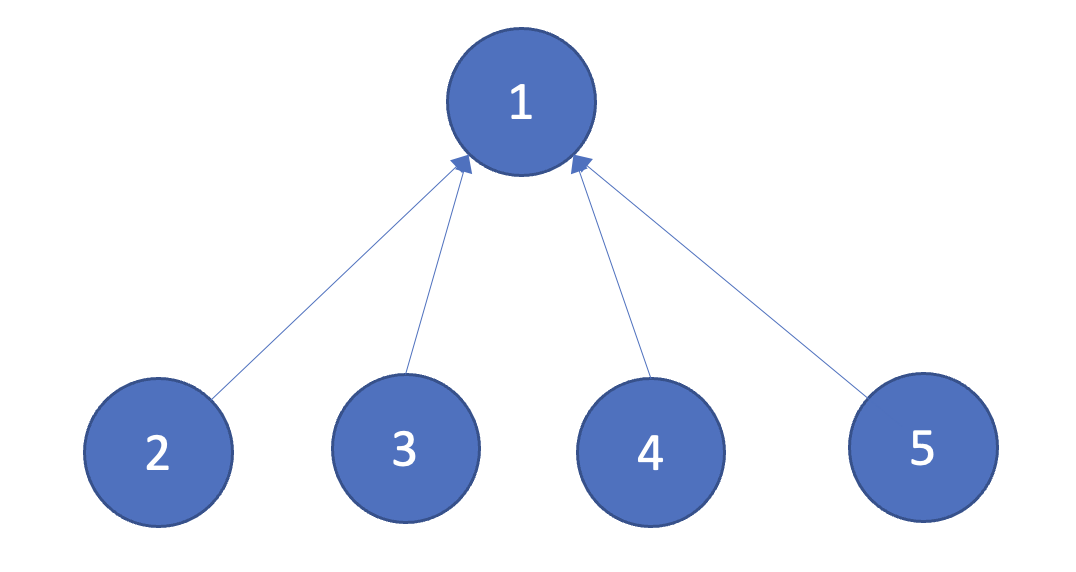

결과적으로 경로 압축 기법을 이용하면 루트 노드에 더욱 빠르게 접근이 가능하여 기존의 알고리즘 대비 시간 복잡도가 개선된다.
개선된 서로소 집합 알고리즘 소스코드는 아래와 같다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else :
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v+1)
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end="")
for i in range(1,v+1):
print(find_parent(parent,i), end=" ")
print()
# 부모 테이블 내용 출력
print("부모 테이블: ", end="")
for i in range(1, v+1):
print(parent[i], end=" ")# input
6 4
1 4
2 3
2 4
5 6
# output
각 원소가 속한 집합: 1 1 1 1 5 5
부모 테이블: 1 1 1 1 5 5
서로소 집합 알고리즘의 시간 복잡도
경로 압축 기법만을 사용한 서로소 집합 알고리즘의 시간 복잡도를 알아보자. 노드의 개수가 V개이고, 최대 V-1개의 union연산과 M개의 find 연산이 가능할 때 경로 압축 기법을 적용한 서로소 집합 알고리즘의 시간 복잡도는 O(V+M(1 + log(2-M/V) V)이다.
예를 들어 노드의 개수가 1,000개이고 union 및 find 연산이 총 100만 번 수행된다면 대략 V + Mlog2V를 개산해서 약 1,000만 번 가량의 연산이 필요하다고 이해하면 된다.
서로소 집합을 활용한 사이클 판별
서로소 집합은 다양한 알고리즘에서 사용될 수 있는데 특히 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다는 특징이 있다. 방향 그래프에서의 사이클 여부는 DFS를 이용하여 판별할 수 있다.
앞에서 설명할 때 union 연산은 그래프에서의 간선으로 표현이 가능하다고 하였다. 따라서 간선을 하나씩 확인하면서 두 노드가 포함되어 있는 집합을 합치는 과정을 반복하는 것을 사이클을 판별할 수 있다.
사이클 판별 알고리즘은 다음과 같다.
1. 각 간선을 확인하며 두 노드의 루트 노드를 확인
1-1. 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행
1-2. 루트 노드가 서로 같다면 사이클(Cycle)이 발생한 것
2. 그래프에 포함되어 있는 모든 간선에 대하여 1.번 과정을 반복
서로소 집합을 활용한 사이클 판별 과정
가장 먼저 모든 노드에 대하여 자기 자신을 부모로 설정하는 형태로 부모 테이블을 초기화 한다.


간선(1, 2)을 확인한다. 노드 1과 노드 2의 루트 노드는 각각 1과 2이다. 더 큰 번호를 갖는 노드 2의 부모 노드를 1로 변경한다.
그래프는 위와 동일하다.

이어서 간선(1, 3)을 확인한다. 노드 1과 노드 3의 루트 노드는 각각 1과 3이다. 더 큰 번호를 갖는 노드 3의 부모 노드를 1로 변경한다.
그래프는 위와 동일하다.

마지막으로 간선(2, 3)을 확인한다. 이때 노드 2와 노드 3은 이미 루트 노드로 '노드 1'을 가지고 있기 때문에 사이클이 발생한다는 것을 알 수 있다.
이러한 사이클 판별 알고리즘은 그래프에 포함되어 있는 간선의 개수가 E개일 때 모든 간선을 하나씩 확인하고, 매 간선에 대하여 union, find 함수를 호출하는 식으로 동작한다. 이 알고리즘은 간선에 방향성이 없는 무향 그래프에서만 적용 가능하다.
서로소 집합을 활용한 사이클 판별 소스코드는 아래와 같다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else :
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v+1)
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
cycle = False
# union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
# 사이클이 발생한 경우 종료
if find_parent(parent, a) == find_parent(parent, b) :
cycle = True
break
# 사이클이 발생하지 않았다면 합집합(union) 수행
else:
union_parent(parent, a, b)
if cycle:
print("사이클이 발생하였습니다.")
else :
print("사이클이 발생하지 않았습니다.")# input
3 3
1 2
1 3
2 3
# output
사이클이 발생했습니다.'정보[Information]' 카테고리의 다른 글
| HTML 블록 태그 / 인라인 태그 (Block Tag / Inline Tag) (0) | 2022.04.06 |
|---|---|
| 신장 트리(Spanning Tree) / 크루스칼 알고리즘(Kruskal Algorithm)(Python - 파이썬) (0) | 2022.03.06 |
| API(Application Programming Interface)란? (0) | 2022.02.20 |
| 클린 코드(Clean Code)를 작성하는 5가지 팁 (3) | 2022.01.23 |
| 정렬 알고리즘(선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬)(Python - 파이썬) (0) | 2022.01.17 |






최근댓글