백준 11404번 문제입니다. (solved.ac)기준 실버 4 문제입니다.
https://www.acmicpc.net/problem/11404
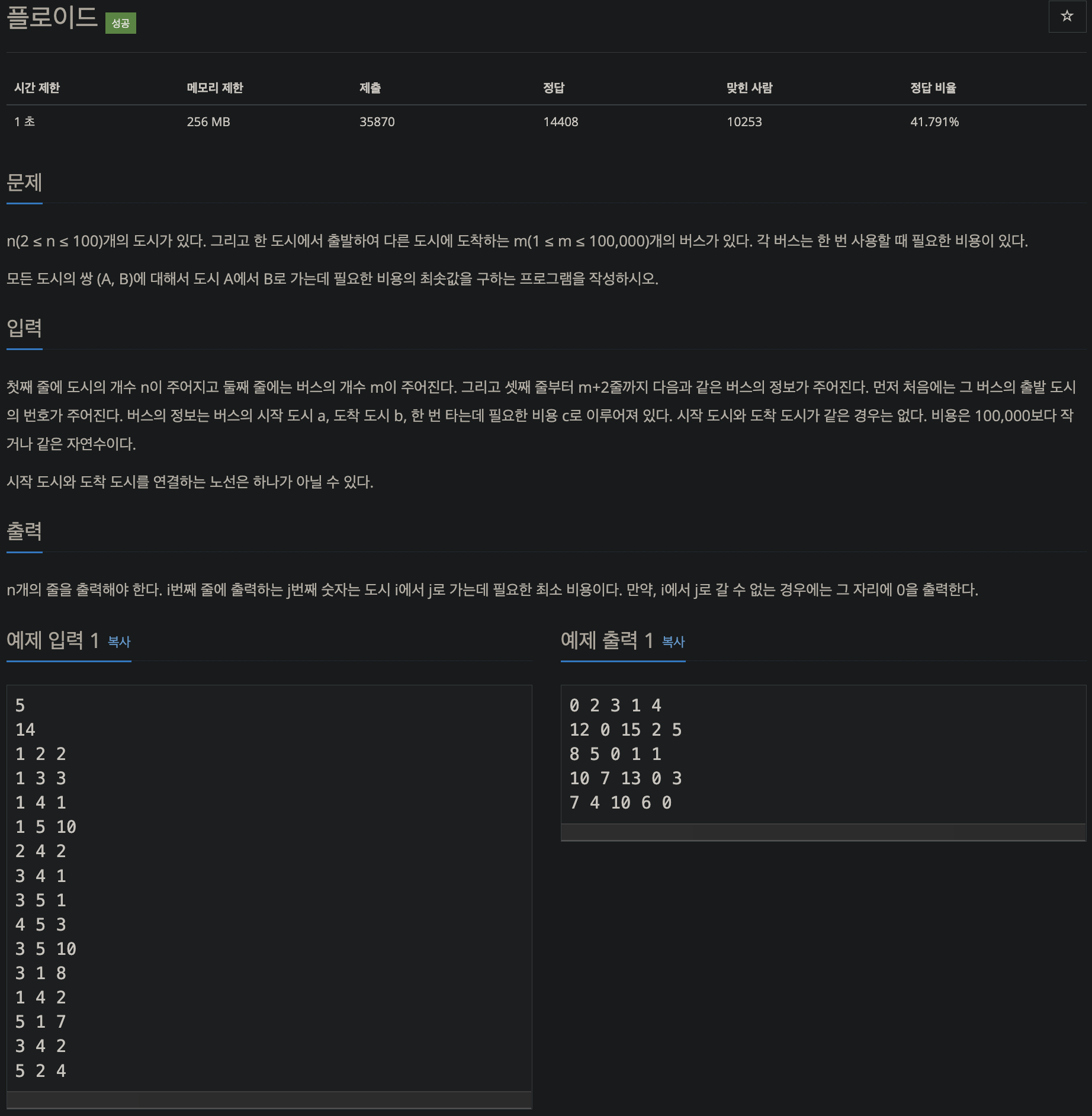
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
문제 접근
시작 노드와 도착 노드가 정해져서 '한 지점에서 다른 특정 지점까지의 최단 거리'를 구할 때 사용하는 다익스트라 알고리즘과는 다르게 플로이드 워셜 알고리즘은 '모든 지점에서 모든 지점까지의 최단 거리'를 구할 때 사용할 수 있습니다.
이 문제 또한 모든 도시의 쌍에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구해야하기 때문에 다익스트라 알고리즘이 아닌 플로이드 워셜 알고리즘으로 접근하였습니다.
다익스트라 알고리즘에서는 '출발 노드가 1개 이므로 다른 모든 노드까지의 최단 거리'를 저장하기 위해 1차원 리스트를 사용하였지만 프롤이드 워셜 알고리즘은 다익스트라 알고리즘과 다르게 '모든 노드에서 다른 모든 노드까지의 최단 거리'를 저장해야 하기때문에 2차원 리스트를 사용해야합니다.
다익스트라 알고리즘은 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택하고 그 노드를 거쳐 가는 경로를 확인하며 최단 거리 테이블을 갱신합니다.
플로이드 워셜 알고리즘도 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행하지만 매번 방문하지 않는 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없습니다. 노드의 개수가 N개일 때 알고리즘 상으로 N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 '현재 노드를 거쳐 가는' 모든 경로를 고려하기 때문에 플로이드 워셜의 알고리즘의 총 시간 복잡도는 O(N^3)입니다.
플로이드 워셜 알고리즘의 각 단계에서는 해당 노드를 거쳐 지나가는 모든 경우를 고려하면 됩니다.
예를 들어 1번 노드를 확인할 때에는 A -> 1번 노드 -> B로 가는 비용을 확인한 후에 최단 거리를 갱신합니다.
A에서 B로가는 최단 경로를 D[A][B]라고 두고 중간에 거쳐가는 노드를 K 라고 잡는다면 아래와 같은 점화식이 도출됩니다.
Dab = min(Dab, Dak + Dkb)
위의 점화식이 의미하는 것은 "A에서 B로 가는 최소 비용" 과 "A에서 k를 거쳐 B로 가는 비용" 중 더 작은 값으로 갱신하겠다는 뜻 입니다.
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])점화식을 파이썬의 코드로 구현하면 위와 같습니다.
정답 코드
import sys
# 10억(무한을 나타내기 위하여 큰 정수로 설정)
INF = int(1e9)
# 도시의 개수(n), 버스의 개수(m)
n = int(input())
m = int(input())
# '모든 노드에서 다른 모든 노드까지의 최단 거리'를 저장하기 위해
# 2차원 리스트를 사용 - 모든 값을 INF로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0
# 버스의 정보를 입력 받음
for _ in range(m):
a, b, c = map(int, sys.stdin.readline().rstrip().split())
if graph[a][b] > c:
graph[a][b] = c
# 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 조건에 맞게 2차원 리스트를 출력
for a in range(1, n + 1):
for b in range(1, n + 1):
if graph[a][b] == INF :
print(0, end =" ")
else :
print(graph[a][b], end=" ")
print()'알고리즘 문제풀이[Algorithm]' 카테고리의 다른 글
| [백준] 4485번 녹색 옷 입은 애가 젤다지?(다익스트라 알고리즘)(Python - 파이썬) (0) | 2022.02.28 |
|---|---|
| [백준] 1504번 특정한 최단 경로(다익스트라 알고리즘)(Python - 파이썬) (0) | 2022.02.27 |
| [백준] 1916번 최소비용 구하기(다익스트라 알고리즘)(Python - 파이썬) (0) | 2022.02.23 |
| [백준] 1753번 최단경로(다익스트라 알고리즘)(Python - 파이썬) (0) | 2022.02.22 |
| [백준] 15829번 Hashing(Python - 파이썬) (0) | 2022.02.19 |








최근댓글