반응형
거듭제곱이란?
거듭제곱이랑 같은 수를 거듭하여 곱한 것으로, 주어진 수를 주어진 횟수만큼 여러 번 곱하는 연산입니다.
위의 사진은 a의 n승(a^n)이라고 하고 a는 밑(주어진 수), n은 지수(주어진 횟수)라고 합니다.
거듭제곱을 구하는 방식들은 아래와 같습니다.
아주 간단한 방식으로 거듭제곱을 구하기 - O(N)
재귀를 이용하여 구하기
fun main() {
println(simplePow(2, 5))
}
// 재귀를 통하여 거듭제곱을 구하는 함수
fun simplePow(a: Int, b: Int): Int {
if (b == 0) {
return 1;
}
return a * simplePow(a, b - 1)
}단순 반복문을 이용하여 구하기
fun main() {
println(simplePow(2, 5))
}
// 단순 반복을 통하여 거듭제곱을 구하는 함수
fun simplePow(a: Int, b: Int): Int {
var aPowerB = 1
for (i in 1..b) {
aPowerB *= a
}
return aPowerB
}위의 방법들은 간단하게 거듭제곱을 구하는 방식입니다.
반복문 혹은 재귀 함수를 사용하여 단순히 a를 n번만큼 곱하여 구할 수 있습니다. 이 때의 시간 복잡도는 O(N)입니다.
거듭제곱의 성질 및 분할정복을 이용하여 효율적으로 거듭제곱 구하기 - O(logN)
거듭제곱의 성질과 그것을 이용하여 분할정복으로 거듭제곱을 구하는 방식의 시간복잡도를 O(logN)으로 줄일 수 있습니다.
거듭제곱의 성질(지수법칙) 중 지수의 덧셈을 이용할 수 있습니다.
이 지수의 덧셈 성질을 이용하여
2^8은

2^9 은

와 같이 표현될 수 있다는 것을 확인할 수 있습니다.
따라서 a^b(a의 b승)가 주어졌을 때
- 지수인 b가 짝수일 경우

- 지수인 b가 홀수일 경우
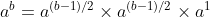
이와 같은 수식이 도출됨을 알 수 있습니다.
이 수식을 재귀를 이용한 함수로 구현한다면
분할정복을 이용한 재귀로 구하기
fun main() {
println(upgradedPow(2, 5))
}
// 재귀를 통하여 거듭제곱을 구하는 함수 (분할정복)
fun upgradedPow(a: Int, b: Int): Int {
if (b == 0) return 1
val aPowerBDividedByTwo = upgradedPow(a, b / 2)
val aPowerBDividedByTwoSquared = aPowerBDividedByTwo * aPowerBDividedByTwo
if (b % 2 == 0) {
return aPowerBDividedByTwoSquared
} else {
return aPowerBDividedByTwoSquared * a
}
}이처럼 거듭제곱의 성질 및 분할정복으로 거듭제곱을 이용하여 구현한다면 시간 복잡도를 O(logN)으로 최적화 시킬 수 있습니다!
반응형
'정보[Information]' 카테고리의 다른 글
| IntelliJ IDEA에서 외부 라이브러리 추가하기(jsoup) (0) | 2022.07.20 |
|---|---|
| Git, Gist에 이미지 혹은 움짤 업로드 하기 (0) | 2022.07.18 |
| git status 명령어 실행 시 파일명이 숫자로 나올 때 해결법 (0) | 2022.06.20 |
| 입력받은 문자열이 정수인지 확인하는 함수[코틀린 - Kotlin] (0) | 2022.06.14 |
| 안드로이드[Android] Check your module classpath for missing or conflicting dependencies 오류 (0) | 2022.05.29 |









최근댓글