반응형
백준 10826번 문제입니다. (solved.ac)기준 실버 4 문제입니다.
https://www.acmicpc.net/problem/10826
10826번: 피보나치 수 4
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
문제
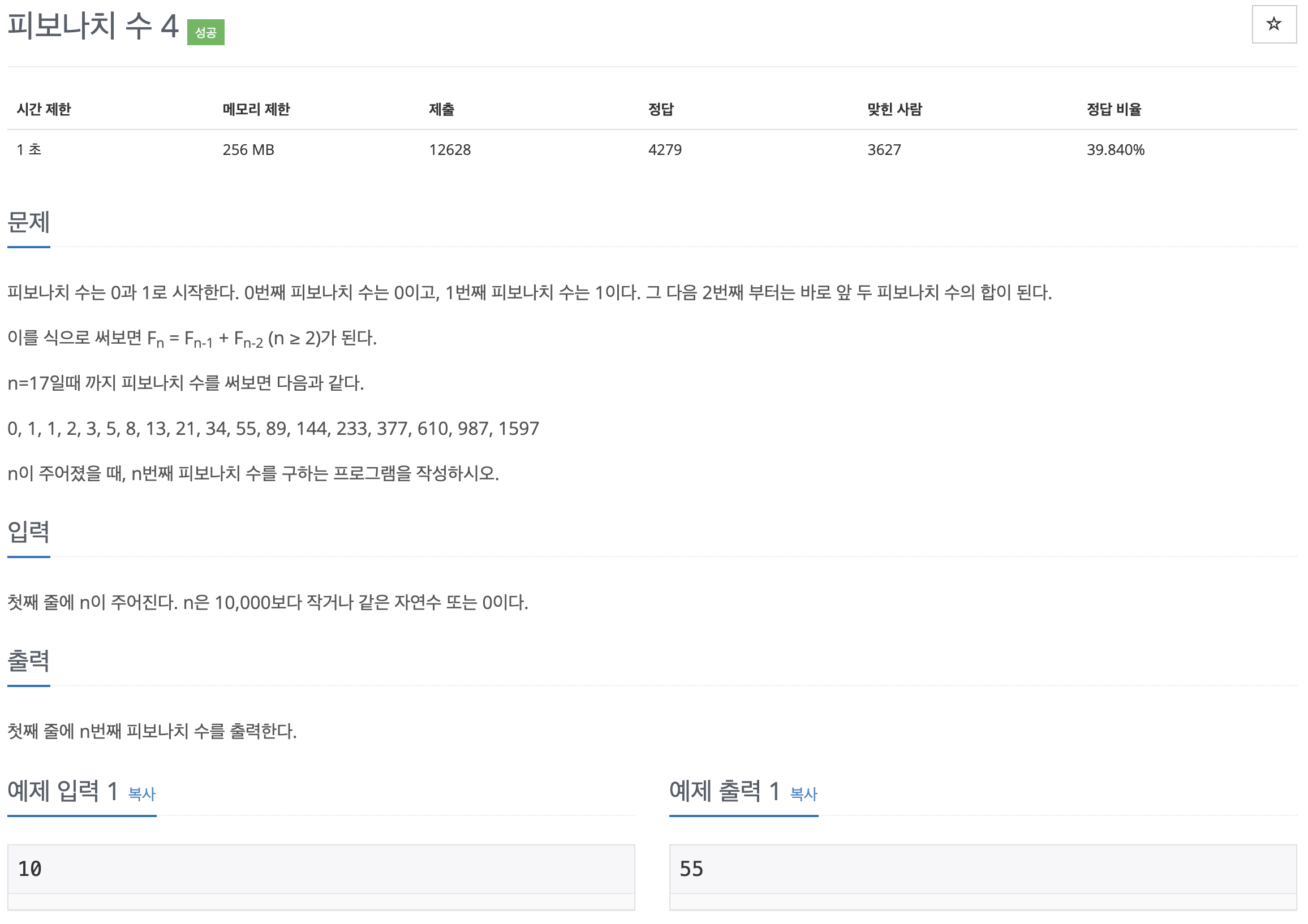
문제 접근
우선 재귀호출로는 시간초과가 발생할 수 있을 것 같아 다이나믹 프로그래밍(DP)방식으로 문제를 풀었습니다.
10,000번째 피보나치 수
3364476487643178326662161200510754331030214846068006390656476997468008144216666236815559551363373402558206533268083615937373479048386526826304089246305643188735454436955982749160660209988418393386465273130008883026923567361313511757929743785441375213052050434770160226475831890652789085515436615958298727968298751063120057542878345321551510387081829896979161312785626503319548714021428753269818796204693609787990035096230229102636813149319527563022783762844154036058440257211433496118002309120828704608892396232883546150577658327125254609359112820392528539343462090424524892940390170623388899108584106518317336043747073790855263176432573399371287193758774689747992630583706574283016163740896917842637862421283525811282051637029808933209990570792006436742620238978311147005407499845925036063356093388383192338678305613643535189213327973290813373264265263398976392272340788292817795358057099369104917547080893184105614632233821746563732124822638309210329770164805472624384237486241145309381220656491403275108664339451751216152654536133311131404243685480510676584349352383695965342807176877532834823434555736671973139274627362910821067928078471803532913117677892465908993863545932789452377767440619224033763867400402133034329749690202832814593341882681768389307200363479562311710310129195316979460763273758925353077255237594378843450406771555577905645044301664011946258097221672975861502696844314695203461493229110597067624326851599283470989128470674086200858713501626031207190317208609408129832158107728207635318662461127824553720853236530577595643007251774431505153960090516860322034916322264088524885243315805153484962243484829938090507048348244932745373262456775587908918719080366205800959474315005240253270974699531877072437682590741993963226598414749819360928522394503970716544315642132815768890805878318340491743455627052022356484649519611246026831397097506938264870661326450766507461151267752274862159864253071129844118262266105716351506926002986170494542504749137811515413994155067125627119713325276363193960690289565028826860836224108205056243070179497617112123306607331005994736687510,000번째 피보나치 수는 위와 같습니다. 글자수를 세어보니 2090자가 되는 것 같습니다.
처음에는 아무생각없이 Long 타입의 mutableList를 사용하여 문제를 풀었는데 당연히 Long 범위를 초과하여 오버플로우가 발생하였습니다.
무한한 수를 계산할 수 있는 BigInteger 형을 사용하여 문제를 해결하였습니다.
BigInteger는 객체를 생성하여 사용할 수 있는데 특이하게 수를 계산하지만 문자열 형태로 값을 넣어주어야 합니다.
0, 1 번째 인덱스에는 초기값을 넣어주고 2부터 입력받은 수(n)번만큼 반복하여 n번째에 있는 피보나치 수를 구하여 출력하도록 구현하였습니다.
정답 코드
import java.math.BigInteger
fun main(){
var num = mutableListOf<BigInteger>()
num.add(BigInteger("0"))
num.add(BigInteger("1"))
var cnt = readln().toInt()
for (no in 2..cnt){
num.add(num[no-2] + num[no-1])
}
print(num[cnt])
}반응형
'알고리즘 문제풀이[Algorithm]' 카테고리의 다른 글
| [백준] 1110 더하기 사이클(Kotlin - 코틀린) (0) | 2022.04.27 |
|---|---|
| [백준] 1966번 프린터 큐(Kotlin - 코틀린) (0) | 2022.04.24 |
| 백준 7568번 덩치(Kotlin - 코틀린) (0) | 2022.04.20 |
| [백준] 4386번 별자리 만들기(크루스칼 알고리즘)(Python - 파이썬) (0) | 2022.03.11 |
| [백준] 1922번 네트워크 연결(크루스칼 알고리즘)(Kruskal Algorithm)(Python - 파이썬) (0) | 2022.03.09 |








최근댓글